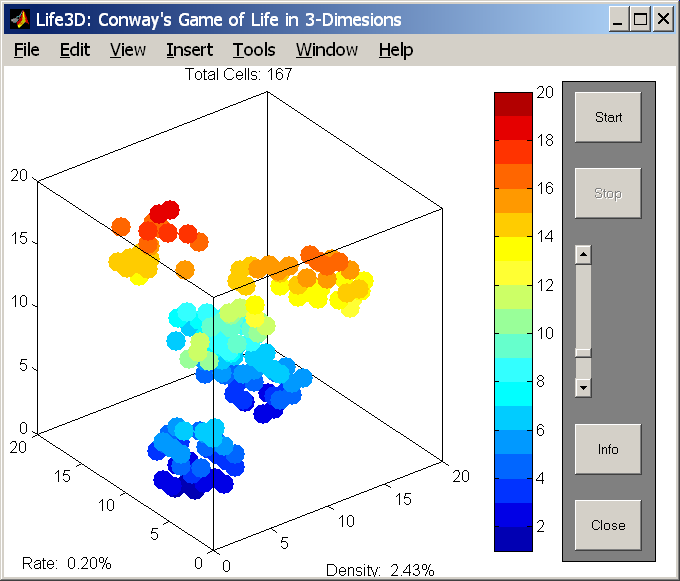
MATLAB’s version of Conway’s Game of Life in 3D
Jul 28th, 2010 | By Leandro | Category: MatlabMy 3D version expansion of Conway’s Game of Life.
function life3D(action) %LIFE3D MATLAB's version of Conway's Game of Life. % "Life" is a cellular automaton invented by John % Conway that involves live and dead cells in a % rectangular, two-dimensional universe. In % MATLAB, the universe is a sparse matrix that % is initially all zero. % % Whether cells stay alive, die, or generate new % cells depends upon how many of their eight % possible neighbors are alive. By using sparse % matrices, the calculations required become % astonishingly simple. We use periodic (torus) % boundary conditions at the edges of the % universe. Pressing the "Start" button % automatically seeds this universe with several % small random communities. Some will succeed % and some will fail. % % Expanded to 3D by: % Leandro Barajas 06-20-2002 L.G.Barajas@ieee.org % % C. Moler, 7-11-92, 8-7-92. % Adapted by Ned Gulley, 6-21-93 % % Copyright 1984-2001 The MathWorks, Inc. % $Revision: 5.9 $ $Date: 2001/04/15 12:03:02 $ % Possible actions: % initialize % start % Information regarding the play status will be held in % the axis user data according to the following table: play= 1; stop=-1; if nargin<1, action='initialize'; end; if strcmp(action,'initialize'), figNumber=figure( ... 'Name','Life3D: Conway''s Game of Life in 3-Dimesions', ... 'NumberTitle','off', ... 'DoubleBuffer','on', ... 'Visible','off', ... 'Color','white', ... 'BackingStore','off'); axes( ... 'Units','normalized', ... 'Position',[0.05 0.05 0.75 0.90], ... 'Visible','off', ... 'DrawMode','fast', ... 'Color','none',... 'NextPlot','add'); % 'NextPlot','replace' ); text(0,0,{'Press the "Start" button to see the Game of Life demo' 'Use the slider to change the number of initial cells.'}, ... 'HorizontalAlignment','center'); axis([-1 1 -1 1]); %=================================== % Information for all buttons labelColor=[0.8 0.8 0.8]; yInitPos=0.90; xPos=0.85; btnLen=0.10; btnWid=0.10; % Spacing between the button and the next command's label spacing=0.05; %==================================== % The CONSOLE frame frmBorder=0.02; yPos=0.05-frmBorder; frmPos=[xPos-frmBorder yPos btnLen+2*frmBorder 0.9+2*frmBorder]; h=uicontrol( ... 'Style','frame', ... 'Units','normalized', ... 'Position',frmPos, ... 'BackgroundColor',[0.50 0.50 0.50]); %==================================== % The START button btnNumber=1; yPos=0.90-(btnNumber-1)*(btnWid+spacing); labelStr='Start'; cmdStr='start'; callbackStr='life3D(''start'');'; % Generic button information btnPos=[xPos yPos-spacing btnLen btnWid]; startHndl=uicontrol( ... 'Style','pushbutton', ... 'Units','normalized', ... 'Position',btnPos, ... 'String',labelStr, ... 'Interruptible','on', ... 'Callback',callbackStr); %==================================== % The STOP button btnNumber=2; yPos=0.90-(btnNumber-1)*(btnWid+spacing); labelStr='Stop'; % Setting userdata to -1 (=stop) will stop the demo. callbackStr='set(gca,''Userdata'',-1)'; % Generic button information btnPos=[xPos yPos-spacing btnLen btnWid]; stopHndl=uicontrol( ... 'Style','pushbutton', ... 'Units','normalized', ... 'Position',btnPos, ... 'Enable','off', ... 'String',labelStr, ... 'Callback',callbackStr); %==================================== % The NumberOfCell Slider labelStr='# Cells'; callbackStr='h=findobj(gcf,''Tag'',''StartCells'');set(h,''Tooltip'',sprintf(''Initial Cells: %4d'',floor(get(h,''Value''))));'; infoHndl=uicontrol( ... 'Style','slider', ... 'Units','normalized', ... 'Position',[xPos btnWid+btnWid*2+0.05 btnLen/4 0.10*3], ... 'String',labelStr, ... 'SliderStep',[.01 .1], ... 'Max',100, ... 'Min',1, ... 'Value',20, ... 'Tooltip','Initial Cells: 20',... 'Tag','StartCells', ... 'Callback',callbackStr); %==================================== % The INFO button labelStr='Info'; callbackStr='life3D(''info'')'; infoHndl=uicontrol( ... 'Style','push', ... 'Units','normalized', ... 'Position',[xPos 0.20 btnLen 0.10], ... 'String',labelStr, ... 'Callback',callbackStr); %==================================== % The CLOSE button labelStr='Close'; callbackStr='close(gcf)'; closeHndl=uicontrol( ... 'Style','push', ... 'Units','normalized', ... 'Position',[xPos 0.05 btnLen 0.10], ... 'String',labelStr, ... 'Callback',callbackStr); % Uncover the figure hndlList=[startHndl stopHndl infoHndl closeHndl]; set(figNumber,'Visible','on', ... 'UserData',hndlList); view(3); StartCells = 20; m = 19; colormap(jet(m)); colorbar; elseif strcmp(action,'start'), objh=findobj(gcf,'Tag','StartCells'); StartCells = get(objh,'Value'); m = 19; cla; axHndl=gca; figNumber=gcf; hndlList=get(figNumber,'Userdata'); startHndl=hndlList(1); stopHndl=hndlList(2); infoHndl=hndlList(3); closeHndl=hndlList(4); set([startHndl closeHndl infoHndl],'Enable','off'); set(stopHndl,'Enable','on'); % ====== Start of Demo set(axHndl, ... 'UserData',play, ... 'DrawMode','fast', ... 'Visible','on'); box off X = zeros(m,m,m); p = -1:1; for count=1:StartCells, kx=floor(rand*(m-4))+2; ky=floor(rand*(m-4))+2; kz=floor(rand*(m-4))+2; X(kx+p,ky+p,kz+p)=(rand(3,3,3)>0.5); end; % The following statements plot the initial configuration. % The "find" function returns the indices of the nonzero elements. plothandle=[]; figure(gcf); hold on colour=jet(m); for k=1:m [i,j] = find(X(:,:,k)); % kd = sub2ind(size(X(i,j,k)),i,j) kd = k(ones(size(i))); if isempty(i) i = 1; j = 1; kd = NaN; end plothandle(k) = line(i,j,kd); set(plothandle(k),'linestyle','none',... 'Marker','.',... 'MarkerSize',20*2,... 'MarkerFaceColor',colour(k,:),... 'MarkerEdgeColor',colour(k,:),... 'EraseMode','normal'); end drawnow axis([0 m+1 0 m+1 0 m+1]); hold off % Whether cells stay alive, die, or generate new cells depends % upon how many of their eight possible neighbors are alive. % Here we generate index vectors for four of the eight neighbors. % We use periodic (torus) boundary conditions at the edges of the universe. n = [m 1:m-1]; e = [2:m 1]; s = [2:m 1]; w = [m 1:m-1]; u = [m 1:m-1]; d = [2:m 1]; rotate3d on while get(axHndl,'UserData')==play, % How many of eight+5+5 neighbors are alive. (only the ones that share at least one border % N = X(n,:,:) + X(s,:,:) + X(:,e,:) + X(:,w,:) + ... % X(n,e,:) + X(n,w,:) + X(s,e,:) + X(s,w,:); % 3D Version % Use Euclidean distance d1 = 1/1; % Adjacent cells (Share 4 vertix) d2 = 1/sqrt(2); % Diagonal cells (Share 2 vertix) d3 = 1/sqrt(3); % Double Diagonal cells (Share 1 vertix) % How many of 9+9+8 neighbors are alive. (Only the ones that share at least one vertix) N = X(n,:,:)*d1 + X(s,:,:)*d1 + X(:,e,:)*d1 + X(:,w,:)*d1 + ... X(n,e,:)*d2 + X(n,w,:)*d2 + X(s,e,:)*d2 + X(s,w,:)*d2 + ... X(n,:,u)*d2 + X(s,:,u)*d2 + X(:,e,u)*d2 + X(:,w,u)*d2 + ... X(n,:,d)*d2 + X(s,:,d)*d2 + X(:,e,d)*d2 + X(:,w,d)*d2 + ... X(n,e,u)*d3 + X(s,e,u)*d3 + X(s,w,u)*d3 + X(n,w,u)*d3 + ... X(n,e,d)*d3 + X(s,e,d)*d3 + X(s,w,d)*d3 + X(n,w,d)*d3 + ... X(:,:,u)*d1 + X(:,:,d)*d1; % A live cell with two live neighbors, or any cell with three % neigbhors, is alive at the next time step. Xold = X; CL = 3.0; % Minimun # cells to create a new one CH = 4.0; % Maximum # cells to create a new one KL = 4.0; % Minimun # cells to kill one X = ( ( ((N >= CL) & (N <= CH)) ) &... % Create cells ~( X & ((N > KL) )) ) ; % Kill cells by overpopulation Xsum = sum(X(:)); if (Xsum>prod(size(X))/8); X = ( X & (rand(size(X))>0.1) ); % Expontaneous cell annihilation end if Xold==X % if no change the exit break; end % Update plot. for k=1:m [i,j] = find(X(:,:,k)); set(plothandle(k),'xdata',i,'ydata',j,'zdata',k(ones(size(i)))); end set(plothandle,'Visible','on'); box on title( sprintf('Total Cells: %d',Xsum)) xlabel(sprintf('Density: %5.2f%%',mean(X(:))*100)) ylabel(sprintf('Rate: %5.2f%%',(mean(X(:))-mean(Xold(:)))*100)) drawnow pause(0.2) end % ====== End of Demo set([startHndl closeHndl infoHndl],'Enable','on'); set(stopHndl,'Enable','off'); elseif strcmp(action,'info'); helpwin(mfilename); end; % if strcmp(action, ... |
 Facebook Profile
Facebook Profile ORCID Profile
ORCID Profile